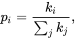El algoritmo de apego preferencial es un interesante algoritmo de predicción de enlaces aplicado al estudio de grafos que toma como base principal una medida para calcular la cercanía de los nodos, en función de un conjunto de vecinos compartidos. A continuación conoceremos un poco más sobre este importante algoritmo que se encuentra disponible en la extensa biblioteca de algoritmos del poderoso Neo4j y desarrollaremos un ejemplo práctico para comprender su funcionalidad.
¿Qué es el apego preferencial?
El algoritmo de apego preferencial se basa en el modelo propuesto por Barabási-Albert que es capaz de generar redes aleatorias sin escala utilizando un mecanismo de conexión preferencial. Esta teoría toma como base fundamental de desarrollo la hipotesis que los sistemas naturales y los creados por el hombre como el internet, las redes de citas académicas y las redes sociales son aproximadamente libres de escala y ciertamente contienen pocos nodos centrales.
Este modelo intenta explicar la existencia de dichos nodos en redes reales.
Este modelo parte de agregar nuevos vértices a la red de uno en uno. Cada nodo agregado a M<M0 nodos existentes con una probabilidad que es proporcional al número de enlaces que los nodos existentes ya poseen. Formalmente la probabilidad ρí de que el nuevo nodo este conectado a otro nodo í es
Donde k(i)K{i} es el grado de nodo I i y la suma se realiza sobre todos los nodos preexistentes j. Es decir, que el denominador de la formula resulta ser el doble del actual número de aristas en la red. Los nodos pertenecientes al grafo que se encuentran fuertemente vinculados tienden a acumular rápidamente aún más enlaces, mientras que es poco probable que nodos con solo unos pocos enlaces sean escogidos como destino para un enlace nuevo.
Los nodos nuevos tienen una «preferencia» para unirse a nodos con alta vinculación.
Algoritmo de apego preferencial
Como ya habéis podido observar, este calculo nos permite determinar cuales nodos dentro de una estructura de un grafo tienen más posibilidades de albergar un nuevo enlace. Con la aplicación del algoritmo que se encuentra en la biblioteca de algoritmos de Neo4j, podemos detectar dichos nodos y estudiarlos a profundidad. Para aplicar este calculo dentro de Neo4j se utiliza una formula que te presentamos a continuación
Donde N(u) es el conjunto de nodos adyacentes a u. Dentro de los resultados que podemos obtener de su calculo tenemos que un valor de 0 indica que dos nodos se encuentran distantes, mientras que los valores más altos indican un mayor nivel de cercanía.
Ejemplo de aplicación
Para comprender más a detalle la aplicación de este importante algoritmo de detección de enlaces, procederemos a construir un grafo en el que se identificarán los vértices con los nombres de personas y se le asignarán características que demuestren las relaciones existentes entre los datos.
Se construye el grafo de la siguiente forma
MERGE (zhen:Person {name: "Zhen"})
MERGE (praveena:Person {name: "Praveena"})
MERGE (michael:Person {name: "Michael"})
MERGE (arya:Person {name: "Arya"})
MERGE (karin:Person {name: "Karin"})
MERGE (zhen)-[:FRIENDS]-(arya)
MERGE (zhen)-[:FRIENDS]-(praveena)
MERGE (praveena)-[:WORKS_WITH]-(karin)
MERGE (praveena)-[:FRIENDS]-(michael)
MERGE (michael)-[:WORKS_WITH]-(karin)
MERGE (arya)-[:FRIENDS]-(karin)Posteriormente ejecutamos el análisis del algoritmo con una consulta en Cypher dirigida a estudiar un par determinado de nodos y obtenemos los resultados respectivos.
MATCH (p1:Person {name: 'Michael'})
MATCH (p2:Person {name: 'Karin'})
RETURN algo.linkprediction.preferentialAttachment(p1, p2) AS scorescore |
|---|
| 6.0 |
Adicionalmente podemos ejecutar consultas especificas por las relaciones que conectan los grafos para estudiar su nivel de vinculación
MATCH (p1:Person {name: 'Michael'})
MATCH (p2:Person {name: 'Karin'})
RETURN algo.linkprediction.preferentialAttachment(p1, p2, {relationshipQuery: "FRIENDS"}) AS scorescore |
|---|
| 1.0 |
Esperamos que esta información sea de utilidad para comprender la importancia de estos algoritmos de grafos.
Visita más de Grapheverywhere para conocer más sobre los algoritmos de análisis de grafos.