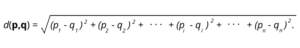El algoritmo de distancia euclidiana es aplicado al estudio de grafos y es extremadamente útil para descubrir la similitud entre dos conjuntos de datos. A continuación conocerás más información importante sobre el algoritmo, cuál es la formula que se aplica para obtener sus valores, descubrirás algunos casos de uso y ejemplos prácticos para comprender a profundidad su aplicabilidad.
¿Qué es el algoritmo de distancia euclidiana?
Este importante algoritmo conocido como algoritmo de distancia euclidiana es la aplicación de una formula matemática que permite medir la distancia en línea recta entre dos puntos en un espacio n-dimensional. La formula que se aplica para poder calcular la similaridad bajo este parámetro es la siguiente:
Para aplicarla de forma eficiente y poder obtener los resultados que necesitamos con precisión en Neo4j contamos con procedimientos y funciones. Las funciones deben utilizarse para calcular valores de conjuntos pequeños de datos como listas o elementos de características sencillas mientras que los procedimientos son implementados en conjuntos de datos de mayor tamaño o complejidad.
Descubramos ahora algunos casos de uso del algoritmo de distancia euclidiana.
Casos de uso del algoritmo de distancia euclidiana
Dentro de las funcionalidades del algoritmo de distancia euclidiana se destaca su utilidad para determinar la similitud entre dos cosas o pares de datos. Partiendo de esto, puede utilizarse la similitud calculada a partir de este algoritmo como parte integral de sistemas de consulta de recomendación. Con ella podemos conseguir esquemas de datos que identifiquen elementos que tengan características similares, como una puntuación o una valoración para que el usuario de la información puede decidir. Un ejemplo de esto puede ser aplicado en un sistema de recomendación de películas para que obtengamos sugerencias en base a las calificaciones recibidas.
Ejemplos de aplicación del algoritmo de distancia euclidiana
Para entender la aplicación de la función del algoritmo de distancia euclidiana probaremos su ejecución en dos listas de números. Es importante destacar que esta distancia se calcula sobre dimensiones no NULL. Al ejecutar la función debemos asegurarnos de ingresar listas que contengan elementos superpuestos.
Para este ejemplo de calculo de similitud incorporamos dos listas codificadas de números como se muestra a continuación:
RETURN algo.similarity.euclideanDistance([3,8,7,5,2,9], [10,8,6,6,4,5]) AS similarity
Results |
similarity |
8.426149773176359 |
Ahora probemos los procedimientos en elementos más complejos del algoritmo de distancia euclidiana utilizando una consulta en Cypher.
En primer lugar construimos un grafo donde asignamos datos y valores:
MERGE (french:Cuisine {name:'French'})
MERGE (italian:Cuisine {name:'Italian'})
MERGE (indian:Cuisine {name:'Indian'})
MERGE (lebanese:Cuisine {name:'Lebanese'})
MERGE (portuguese:Cuisine {name:'Portuguese'})
MERGE (british:Cuisine {name:'British'})
MERGE (mauritian:Cuisine {name:'Mauritian'})
MERGE (zhen:Person {name: "Zhen"})
MERGE (praveena:Person {name: "Praveena"})
MERGE (michael:Person {name: "Michael"})
MERGE (arya:Person {name: "Arya"})
MERGE (karin:Person {name: "Karin"})
MERGE (praveena)-[:LIKES {score: 9}]->(indian)
MERGE (praveena)-[:LIKES {score: 7}]->(portuguese)
MERGE (praveena)-[:LIKES {score: 8}]->(british)
MERGE (praveena)-[:LIKES {score: 1}]->(mauritian)
MERGE (zhen)-[:LIKES {score: 10}]->(french)
MERGE (zhen)-[:LIKES {score: 6}]->(indian)
MERGE (zhen)-[:LIKES {score: 2}]->(british)
MERGE (michael)-[:LIKES {score: 8}]->(french)
MERGE (michael)-[:LIKES {score: 7}]->(italian)
MERGE (michael)-[:LIKES {score: 9}]->(indian)
MERGE (michael)-[:LIKES {score: 3}]->(portuguese)
MERGE (arya)-[:LIKES {score: 10}]->(lebanese)
MERGE (arya)-[:LIKES {score: 10}]->(italian)M
ERGE (arya)-[:LIKES {score: 7}]->(portuguese)
MERGE (arya)-[:LIKES {score: 9}]->(mauritian)
MERGE (karin)-[:LIKES {score: 9}]->(lebanese)
MERGE (karin)-[:LIKES {score: 7}]->(italian)
MERGE (karin)-[:LIKES {score: 10}]->(portuguese)Lo siguiente devolverá los resultados de distancia euclidiana de los nodos identificados como Zhen y Praveena:
MATCH (p1:Person {name: 'Zhen'})-[likes1:LIKES]->(cuisine)MATCH (p2:Person {name: "Praveena"})-[likes2:LIKES]->(cuisine)
RETURN p1.name AS from, p2.name AS to, algo.similarity.euclideanDistance(collect(likes1.score), collect(likes2.score))
AS similarityResults | ||
from | to | similarity |
"Zhen" | "Praveena" | 6.708203932499369 |
Lo siguiente devolverá la distancia euclidiana del nodo identificado como Zhen y las otras personas que tienen un elemento en común:
MATCH (p1:Person {name: 'Zhen'})-[likes1:LIKES]->(cuisine)
MATCH (p2:Person)-[likes2:LIKES]->(cuisine) WHERE p2 <> p1
RETURN p1.name AS from,
p2.name AS to,
algo.similarity.euclideanDistance(collect(likes1.score), collect(likes2.score)) AS similarity
ORDER BY similarity DESCTable 7.127. Results | ||
from | to | similarity |
"Zhen" | "Praveena" | 6.708203932499369 |
"Zhen" | "Michael" | 3.605551275463989 |
Ejemplo de procedimientos del algoritmo
El algoritmo de distancia euclidiana es un algoritmo simetrico que permite evaluar la similitud entre todos los pares de elementos que conforman un grafo. Esto significa que si calculamos la similitud del elemento 1 con respecto al elemento 2, obtendremos automáticamente la similitud del elemento 2 con respecto al 1. Por lo tanto, podemos calcular la puntuación para cada par de nodos una vez y no calculamos la similitud de los elementos con ellos mismos.
La distancia euclidiana solo se calcula sobre dimensiones no NULL. Los procedimientos deben recibir la misma cantidad de datos para todos los elementos y deben rellenarse cuando sea necesario.
Para ejecutar este ejemplo procedemos a crear un grafo de la siguiente forma:
MERGE (french:Cuisine {name:'French'})
MERGE (italian:Cuisine {name:'Italian'})
MERGE (indian:Cuisine {name:'Indian'})
MERGE (lebanese:Cuisine {name:'Lebanese'})
MERGE (portuguese:Cuisine {name:'Portuguese'})
MERGE (british:Cuisine {name:'British'})
MERGE (mauritian:Cuisine {name:'Mauritian'})MERGE (zhen:Person {name: "Zhen"})
MERGE (praveena:Person {name: "Praveena"})
MERGE (michael:Person {name: "Michael"})
MERGE (arya:Person {name: "Arya"})
MERGE (karin:Person {name: "Karin"})MERGE (praveena)-[:LIKES {score: 9}]->(indian)
MERGE (praveena)-[:LIKES {score: 7}]->(portuguese)
MERGE (praveena)-[:LIKES {score: 8}]->(british)
MERGE (praveena)-[:LIKES {score: 1}]->(mauritian)MERGE (zhen)-[:LIKES {score: 10}]->(french)
MERGE (zhen)-[:LIKES {score: 6}]->(indian)
MERGE (zhen)-[:LIKES {score: 2}]->(british)MERGE (michael)-[:LIKES {score: 8}]->(french)
MERGE (michael)-[:LIKES {score: 7}]->(italian)
MERGE (michael)-[:LIKES {score: 9}]->(indian)
MERGE (michael)-[:LIKES {score: 3}]->(portuguese)
MERGE (arya)-[:LIKES {score: 10}]->(lebanese)
MERGE (arya)-[:LIKES {score: 10}]->(italian)
MERGE (arya)-[:LIKES {score: 7}]->(portuguese)
MERGE (arya)-[:LIKES {score: 9}]->(mauritian)MERGE (karin)-[:LIKES {score: 9}]->(lebanese)
MERGE (karin)-[:LIKES {score: 7}]->(italian)
MERGE (karin)-[:LIKES {score: 10}]->(portuguese)
Ahora ejecutaremos el algoritmo para obtener la similitud entre los pares de vértices que componen el grafo y obtendremos los resultados respectivos:
MATCH (p:Person), (c:Cuisine)
OPTIONAL MATCH (p)-[likes:LIKES]->(c)
WITH {item:id(p), weights: collect(coalesce(likes.score, algo.NaN()))} as userData
WITH collect(userData) as data
CALL algo.similarity.euclidean.stream(data)
YIELD item1, item2, count1, count2, similarity
RETURN algo.asNode(item1).name AS from, algo.asNode(item2).name AS to, similarity
ORDER BY similarity
Table 7.128. Results | ||
from | to | similarity |
"Zhen" | "Arya" | 0.0 |
"Zhen" | "Karin" | 0.0 |
"Praveena" | "Karin" | 3.0 |
"Zhen" | "Michael" | 3.605551275463989 |
"Praveena" | "Michael" | 4.0 |
"Arya" | "Karin" | 4.358898943540674 |
"Michael" | "Arya" | 5.0 |
"Zhen" | "Praveena" | 6.708203932499369 |
"Michael" | "Karin" | 7.0 |
"Praveena" | "Arya" | 8.0 |
En los resultados de la tabla producto de la ejecución del algoritmo podemos obtener que los vértices pares descritos bajo los nombres de Zhen y Arya, y Zhen y Karin tienen las preferencias alimentarias más similares, con una distancia de 0.0, indicándonos que son extremadamente similares. mientras más bajo el número, mayor similitud.
Esperamos que estos ejemplos sean de utilidad para comprender la funcionalidad de este algoritmo.
Visita más de Grapheverywhere para conocer más sobre algoritmos de grafos.