El algoritmo de rutas cortas K de Yen calcula rutas sin bucles K de fuente única en un grafo con pesos de relación no negativos. Este tipo de tiene potencialidades excepcionales para ser implementados en entornos complejos de relaciones entre nodos. A continuación conoceremos los orígenes de este algoritmo, sus principales casos de uso, restricciones y un ejemplo práctico desarrollado en Neo4j para comprender cómo se aplica al análisis de grafos.

¿Qué es el algoritmo de rutas K de Yen?

El algoritmo de rutas más cortas K del Yen es el que se encarga de calcular las rutas sin ningún bucle K, más cortas desde una fuente o vértice único desde un grafo que posea pesos de relación no negativos. Este algoritmo fue definido por Jin Y Yen en el año 1971 en un trabajo académico titulado «Encontrando el camino más corto K sin bucles en una red.

En el entorno de Neo4j se utiliza una implementación especial de este algoritmo que utiliza en primer lugar el algoritmo de Dijkstra para determinar la ruta más corta dentro de un grafo y posteriormente con este algoritmo se procede a encontrar las desviaciones producto de K-1 de las rutas más cortas. Ahora que concemos más sobre su origen y funcionamiento, procedamos a descubrir sus principales casos de uso y restricciones.

Casos de uso del algoritmo y restricciones

Dentro de los más destacados casos de uso del algoritmo de rutas cortas K de Yen podemos encontrar que es implementado para optimizar el seguimiento de objetos múltiples dentro de un grafo. Esto mediante la formalización de los movimientos de los objetivos, estudiando de forma dinámica el flujo de las relaciones dentro del grafo. Adicionalmente este algoritmo puede ser utilizado para estudiar el enrutamiento alternativo de redes de circulación terrestre para mejorar las recomendaciones de las rutas K al usuario.

En cuanto a las restricciones de uso del algoritmo, este no debe utilizarse cuando necesitemos considerar pesos negativos dentro de las estimaciones. Al igual que algoritmos similares de búsqueda de rutas optimas o cortas, no admite el hecho de que agregar relaciones pudiese hacer que una ruta sea más corta.

Ejemplo en Neo4j

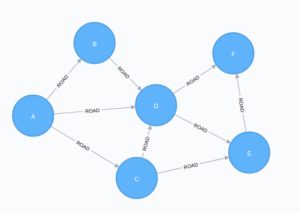
Dentro del entorno de Neo4j podemos desarrollar cálculos precisos con este algoritmo tan importante. A continuación desarrollaremos una simulación de análisis sobre un grafo. En primer lugar desarrollamos en cypher la estructura de un grafo similar al que mostramos a continuación:

Creamos el grafo designando nodos y un costo o peso especifico de la siguiente forma:

MERGE (a:Loc {name:'A'})
MERGE (b:Loc {name:'B'})
MERGE (c:Loc {name:'C'})
MERGE (d:Loc {name:'D'})
MERGE (e:Loc {name:'E'})
MERGE (f:Loc {name:'F'})

MERGE (a)-[:ROAD {cost:50}]->(b)
MERGE (a)-[:ROAD {cost:50}]->(c)
MERGE (a)-[:ROAD {cost:100}]->(d)
MERGE (b)-[:ROAD {cost:40}]->(d)
MERGE (c)-[:ROAD {cost:40}]->(d)
MERGE (c)-[:ROAD {cost:80}]->(e)
MERGE (d)-[:ROAD {cost:30}]->(e)
MERGE (d)-[:ROAD {cost:80}]->(f)
MERGE (e)-[:ROAD {cost:40}]->(f);

Posteriormente ejecutamos el algoritmo y nos devuelve los siguientes resultados:

MATCH (start:Loc{name:'A'}), (end:Loc{name:'F'})
CALL algo.kShortestPaths.stream(start, end, 3, 'cost' ,{})

YIELD index, nodeIds, costs
RETURN [node in algo.getNodesById(nodeIds) | node.name] AS places,
       costs,
       reduce(acc = 0.0, cost in costs | acc + cost) AS totalCost

places	costs	totalCost
[«A», «B», «D», «E», «F»]	[50.0, 40.0, 30.0, 40.0]	160.0
[«A», «C», «D», «E», «F»]	[50.0, 40.0, 30.0, 40.0]	160.0
[«A», «B», «D», «F»]	[50.0, 40.0, 80.0]	170.0

En este ejemplo no obtenemos de forma clara rutas predeterminadas, por lo que debemos hacer que el algoritmo de forma forzada nos devuelva una ruta especifica:

MATCH (start:Loc{name:'A'}), (end:Loc{name:'F'})
CALL algo.kShortestPaths.stream(start, end, 3, 'cost', {path: true})
YIELD path
RETURN path
LIMIT 1

Ejecutamos nuevamente el algoritmo

MATCH (start:Loc{name:'A'}), (end:Loc{name:'F'})
CALL algo.kShortestPaths(start, end, 3, 'cost' ,{})
YIELD resultCount
RETURN resultCount

En este caso el algoritmo nos devuelve los siguientes resultados:

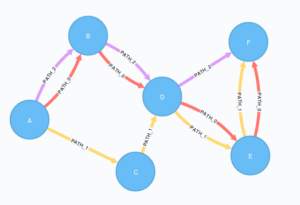
MATCH p=()-[r:PATH_0|:PATH_1|:PATH_2]->() RETURN p LIMIT 25

El algoritmo nos muestra dentro del grafo 3 rutas diferentes, siendo la más corta la ruta que se origina desde a hasta b.

Esperamos que esta información sea útil para comprender el funcionamiento de estos algoritmos.

Visita más de Grapheverywhere para conocer más sobre los algoritmos de grafos.