La centralidad de vector propio es una medida muy interesante aplicada mediante algoritmos que miden la influencia transitiva o la conectividad que posee un nodo dentro de un grafo. Este algoritmo evalúa las relaciones de los nodos con un esquema de puntuaciones. Los nodos de alta puntuación representan a aquellos vértices que tienen mayores conexiones y por lo tanto poseen un nivel de relevancia superior.
A continuación descubriremos algunos datos importantes sobre estos algoritmos, sus potencialidades de uso y un ejemplo básico de aplicación en Neo4j para comprender mejor su funcionamiento.
¿Qué son los algoritmos de centralidad de vector propio?
Los algoritmos de centralidad de vector propio son aquellos que están diseñados especialmente para calcular el grado de influencia de un nodo o vértice dentro de un grafo. Este concepto nace en 1986 con la propuesta académica desarrollada por Phillip Bonacich.
Dentro de este esquema los nodos que poseen una alta puntuación en la escala de evaluación de esta medida de centralidad de vector propio están conectados de forma más eficiente dentro de un grafo determinado o posee un alto nivel de conexiones y por lo tanto son buenos candidatos para difundir información ya que su nivel de conectividad garantiza altas probabilidades de propagación.
El cálculo del Page Rank de Google es una variante de esta medida.
Casos de uso de los algoritmos de centralidad de vector propio
El calculo realizado por este algoritmo funciona de forma similar al Page Rank de Google. Es por esto que la medida de centralidad de vector propio puede ser también utilizada para determinar la relevancia de determinados conjuntos de datos dentro de un grafo. Con este calculo desarrollando un análisis en redes sociales podemos determinar cuales cuentas poseen mayor grado de influencia.
Dentro de un grafo podemos evaluar que nodo comparte conexiones comunes con otros nodos y desarrollar propuestas detalladas y esfuerzos de mercadeo. También pueden desarrollarse modelos predictivos de flujo de tráfico y transito de personas en espacios geográficos determinados, para plantear soluciones de movilidad urbana en intersecciones y carreteras.
De igual manera que el PageRank estos algoritmos pueden ser utilizados para detectar relaciones ocultas o difíciles de identificar dentro de sistemas bancarios o de seguros, ayudando a la prevención de fraudes.
Ejemplo de aplicación del algortimo
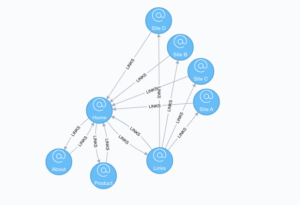
Desarrollaremos a continuación un ejemplo de aplicación del algoritmo para comprender mejor como este relaciona el calculo. El caso de estudio será aplicado a un sitio web y a las paginas internas que están entrelazadas con el.
En primer lugar construimos el grafo con la información:
MERGE (home:Page {name:'Home'})
MERGE (about:Page {name:'About'})
MERGE (product:Page {name:'Product'})
MERGE (links:Page {name:'Links'})
MERGE (a:Page {name:'Site A'})
MERGE (b:Page {name:'Site B'})
MERGE (c:Page {name:'Site C'})
MERGE (d:Page {name:'Site D'})
MERGE (home)-[:LINKS]->(about)
MERGE (about)-[:LINKS]->(home)
MERGE (product)-[:LINKS]->(home)
MERGE (home)-[:LINKS]->(product)
MERGE (links)-[:LINKS]->(home)
MERGE (home)-[:LINKS]->(links)
MERGE (links)-[:LINKS]->(a)
MERGE (a)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(b)
MERGE (b)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(c)
MERGE (c)-[:LINKS]->(home)
MERGE (links)-[:LINKS]->(d)Ejecutamos el calculo del algoritmo en Neo4j y obtenemos este primer resultado:
CALL algo.eigenvector.stream('Page', 'LINKS', {})
YIELD nodeId, score
RETURN algo.asNode(nodeId).name AS page,score
ORDER BY score DESCCompletamos el calculo del algoritmo y este nos devuelve el siguiente resultado
CALL algo.eigenvector('Page', 'LINKS', {write: true, writeProperty:"eigenvector"})
YIELD nodes, iterations, loadMillis, computeMillis, writeMillis, dampingFactor, write, writePropertyPara comprender el resultado, obtenemos una tabla que nos indica directamente el valor obtenido por cada página.
| Name | Eigenvector Centrality |
|---|---|
| Home | 31.45819 |
| About | 14.40379 |
| Product | 14.40379 |
| Links | 14.40379 |
| Site A | 6.572370000000001 |
| Site C | 6.572370000000001 |
| Site D | 6.572370000000001 |
| Site B | 6.572370000000001 |
Como es lógico al tratarse de un sitio web y sus paginas complementarias, la sección de inicio tiene el valor más alto ya que esta conectado a las demás en su totalidad. Este ejemplo permite comprender de mejor manera que no solo es importante la cantidad de conexiones salientes o entrantes, sino la relevancia de la pagina que da origen a los enlaces.
Esperamos que esta información fuese de utilidad para comprender el funcionamiento de este importante algoritmo.
Visita más de Grapheveryhere para conocer la mejor información sobre algoritmos de grafos.