La centralidad por cercanía o proximidad es un concepto interesante que se encuentra enmarcado en la teoría de grafos y su funcionamiento esta centrado en los algoritmos de centralidad. Esta se encarga de determinar las rutas más eficientes que se deben recorrer para llegar desde un nodo a otro dentro de un grafo. Este calculo suele ser utilizado para estimar la velocidad con la que una información puede ser difundida desde un nodo, hacia el resto de los nodos que componen un grafo determinado.

A continuación descubriremos qué son los algoritmos de centralidad por cercanía, algunos casos de uso, sus restricciones y un ejemplo para comprender su funcionamiento.

¿Qué son los algoritmos de centralidad por cercanía?

Como ya hemos dicho en la introducción de este post, la centralidad por cercanía o proximidad es una forma de detectar vértices que están dentro de la estructura de un grafo y que tienen la posibilidad de difundir información de forma eficiente. Este calculo de proximidad de un nodo, también permite conocer su lejanía promedio (distancia inversa) del resto de los nodos.

Los vértices con un puntaje superior de cercanía poseen distancias más cortas que el resto de los nodos que conforman el grafo.

Dentro del análisis que realiza el algoritmo de centralidad por cercanía se calcula por cada uno de los vértices la suma de sus distancias con el resto de los nodos, tomando en cuenta el cálculo de las rutas más cortas entre todos los pares de nodos. La suma resultante de este calculo se invierte para determinar la puntuación de cercanía o proximidad de dicho nodo.

Casos de uso

La centralidad de cercanía es tomada en cuenta para investigar el comportamiento de los individuos dentro de un esquema de redes organizacionales. Con esto se puede determinar quienes están en una posición favorable de controlar y difundir de forma eficiente la información necesaria y el uso de recursos vitales dentro de una empresa.

Adicionalmente los resultados de estos algoritmos pueden ser interpretados como una estimación de llegada de la información transmitida dentro de un canal de telecomunicaciones. Sirviendo también para estimar las rutas más cortas de servicios de entrega de paqueteria. Siguiendo este principio estos algoritmos de proximidad pueden ser utilizados en redes sociales para saber la velocidad de propagación de datos a través de rutas cortas.

Restricciones de aplicación

Es importante destacar que a pesar de ser unos algoritmos altamente funcionales, estos funcionan de forma óptima en grafos conectados, es decir, que su aplicación en grafos no conectados pueden arrojarnos algunos errores de análisis. Pudiésemos obtener una distancia infinita entre dos nodos en componentes conectados por separado. Al ocurrir esto se estaría otorgando una puntuación de centralidad de cercanía infinita cuando hagamos la sumatoria de las distancias de un vértice determinado.

Ejemplo

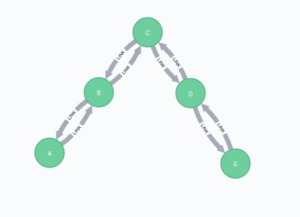
A continuación te presentamos un ejemplo construido en Neo4j para entender de mejor manera el funcionamiento del algoritmo. En primer lugar construimos un grafo de la siguiente forma:

MERGE (a:Node{id:"A"})
MERGE (b:Node{id:"B"})
MERGE (c:Node{id:"C"})
MERGE (d:Node{id:"D"})
MERGE (e:Node{id:"E"})

MERGE (a)-[:LINK]->(b)
MERGE (b)-[:LINK]->(a)
MERGE (b)-[:LINK]->(c)
MERGE (c)-[:LINK]->(b)
MERGE (c)-[:LINK]->(d)
MERGE (d)-[:LINK]->(c)
MERGE (d)-[:LINK]->(e)
MERGE (e)-[:LINK]->(d);

Posteriormente ejecutamos el algoritmo y nos muestra el siguiente resultado:

CALL algo.closeness.stream('Node', 'LINK')
YIELD nodeId, centrality

RETURN algo.asNode(nodeId).id AS node, centrality
ORDER BY centrality DESC
LIMIT 20;

Al terminar de ejecutarse el calculo del algoritmo devuelve este resultado:

CALL algo.closeness('Node', 'LINK', {write:true, writeProperty:'centrality'})
YIELD nodes,loadMillis, computeMillis, writeMillis;

Podemos obtener los datos también en una tabla similar a esta:

Name	Centrality weight
C	0.6666666666666666
B	0.5714285714285714
D	0.5714285714285714
A	0.4
E	0.4

Dentro de esta simulación tenemos que el nodo identificado como C es el vértice con mayor peso de centralidad por cercanía, siendo este el de mayor funcionalidad para desplegar información dentro del grafo.

Esperamos que esta información sea de utilidad para comprender la importancia de estos algoritmos.

Visita más de Grapheverywhere para descubrir más contenido interesante sobre algoritmos.