El article rank es uno de los algoritmos de grafos más interesantes que está almacenado dentro de la biblioteca de algoritmos de grafos del potente Neo4j. Se trata de una variante elaborada a través de los postulados base del Page Rank, que busca medir la influencia transitiva o el nivel de conectividad de los vértices contenidos en un grafo. Este algoritmo a pesar de estar incluido dentro de la base de Neo4j es totalmente experimental y no esta reconocido oficialmente. 

Conozcamos a continuación los datos más importantes de el article rank. 

Article rank 

El article rank como ya hemos dicho es una variante elaborada a través de la base del Page Rank que es el algoritmo que rige la valoración del motor de búsqueda de Google, pero teniendo una diferencia sustancial. En este caso el article rank asume que las relaciones existentes entre los nodos que poseen escasos o bajos grados de salida son más importantes que las relaciones de los nodos con un grado de salida más elevado. 

Este funcionamiento casi inverso de la valoración y medición del algoritmo hace que este caso sea estudiado y ampliamente debatido en la comunidad científica y tecnológica. A profundidad puedes conocer el paper académico sobre el article rank en el reconocido portal research gate. 

Puedes ejecutar análisis sobre conjuntos de datos y disfrutar de todas sus potencialidades desde las librerias de Neo4j. 

Cómo funciona el Article Rank 

Este algoritmo funciona básicamente con la fórmula que te presentamos a continuación: 

AR(A) = (1-d) + d (AR(T1)/(C(T1) + C(AVG)) + ... + AR(Tn)/(C(Tn) + C(AVG))

Dentro de esta formulación se asume que A tiene páginas desde T1 a Tn y que apuntan a ella en forma de citas o referenciaciones. En este caso “d” es un factor que funciona en clave de amortiguación, estableciéndose sus valores en un rango que comprende desde 0 hasta 1. Por lo general, de forma arbitraria se le establece como valor estándar 0.85. 

Adicionalmente dentro de la formulación matemática se define C(A) como el número de enlaces que salientes de la página A, mientras que C (AVG) se definen como el número promedio de enlaces que figuran como salientes hacia todas las páginas. 

Diferencias centrales con el Page Rank

Como ya os hemos explicado en párrafos anteriores, el article rank funciona de manera similar al Page Rank de Google, pero con una diferencia importante ya que este reduce el sesgo de puntuación que ocurre dentro el Page Rank que suele asignar puntuaciones más altas a los nodos con relaciones de nodos que tienen escasas relaciones salientes. 

En el esquema de funcionamiento del Page Rank se cuentan todos los puntajes pertenecientes a los vértices entrantes y este número es dividido por el número de enlaces salientes para cada página entrante, en cambio, el article rank asigna un puntaje contando todos los puntajes que pertenecen a los nodos entrantes y los divide en este caso por el número promedio de enlaces salientes sumado al número de enlaces salientes para cada página entrante. 

Estas diferencias sustanciales con la formulación y el funcionamiento del algoritmo nos permite obtener una valoración más neutral y apegada a  la realidad de los enlaces a considerar. Esta característica en especial ha logrado que el article rank sea utilizado ampliamente para analizar valoraciones de citas en trabajos científicos y académicos en diferentes universidades del mundo. 

Ejemplo de aplicación de Article Rank en Neo4j 

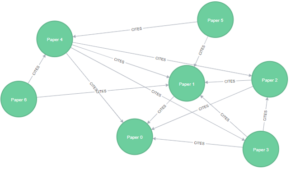
A continuación te presentamos un ejemplo base del funcionamiento del algoritmo article rank, Para este ejercicio de ejemplo se toman 6 artículos o papers académicos y en base a las citas cruzadas que se den dentro del grafo, el algoritmo valorará cual de los papers tiene más valor.

Paso 1 – Creamos el grafo con la información a analizar.

MERGE (paper0:Paper {name:'Paper 0'})
MERGE (paper1:Paper {name:'Paper 1'})
MERGE (paper2:Paper {name:'Paper 2'})
MERGE (paper3:Paper {name:'Paper 3'})
MERGE (paper4:Paper {name:'Paper 4'})
MERGE (paper5:Paper {name:'Paper 5'})
MERGE (paper6:Paper {name:'Paper 6'})

MERGE (paper1)-[:CITES]->(paper0)

MERGE (paper2)-[:CITES]->(paper0)
MERGE (paper2)-[:CITES]->(paper1)

MERGE (paper3)-[:CITES]->(paper0)
MERGE (paper3)-[:CITES]->(paper1)
MERGE (paper3)-[:CITES]->(paper2)

MERGE (paper4)-[:CITES]->(paper0)
MERGE (paper4)-[:CITES]->(paper1)
MERGE (paper4)-[:CITES]->(paper2)
MERGE (paper4)-[:CITES]->(paper3)

MERGE (paper5)-[:CITES]->(paper1)
MERGE (paper5)-[:CITES]->(paper4)

MERGE (paper6)-[:CITES]->(paper1)
MERGE (paper6)-[:CITES]->(paper4)

Paso 2 – Ejecutamos el algoritmo y obtenemos el siguiente resultado

CALL algo.articleRank.stream('Paper', 'CITES', {iterations:20, dampingFactor:0.85})
YIELD nodeId, score
RETURN algo.asNode(nodeId).name AS page,score
ORDER BY score DES

Paso 3 – Proseguimos la ejecución del algoritmo

CALL algo.articleRank('Paper', 'CITES',
  {iterations:20, dampingFactor:0.85, write: true,writeProperty:"pagerank"})
YIELD nodes, iterations, loadMillis, computeMillis, writeMillis, dampingFactor, write, writeProperty

Lo que nos arrojaría una tabla de resultados similar a la que te mostramos a continuación:

Name	ArticleRank
Paper 0	0.34616300000000005
Paper 1	0.319422
Paper 4	0.213733
Paper 2	0.21089400000000003
Paper 3	0.18026850000000003
Paper 5	0.15000000000000002
Paper 6	0.15000000000000002

Estos resultados nos indican que el documento 0 es el de mayor relevancia dentro del grafo, aunque sea citado menos veces que el documento numero 1. Gracias a las propiedades del algoritmo se puede ponderar mejor la relevancia de que sea el documento 0 funja como punto de partida a las demás citas.

Esperamos que esta información sea de utilidad para comprender mejor los postulados y el funcionamiento de importante algoritmo. 

Visita más de Grapheverywhere para conocer todo lo que necesitas sobre algoritmos de centralidad.