El algoritmo de louvain forma parte de la familia de formulaciones matemáticas destinadas a detectar comunidades en redes. Este algoritmo aplica un método que busca optimizar la modularidad existente en un rango de valor establecido desde -1 a 1, comparando la densidad de aristas dentro y fuera de la comunidad de datos establecida. Veamos a continuación una definición un poco más profunda de este importante tipo de algoritmo, sus casos de uso y un ejemplo operacional.
¿Qué es el algoritmo de Louvain?
El algoritmo de Louvain esta basado en la modularidad de los datos. Este realiza una evaluación del conjunto de datos y compara la densidad de aristas que están presentes dentro o fuera de la comunidad. Al optimizar este valor de iteración se obtiene un estimado de agrupación de los nodos que pertenecen a una red.
El algoritmo es aplicado en un método que consiste de dos pasos que buscan estructurar las comunidades de datos conectados. En primer lugar se desarrolla una asignación directa sobre los nodos que conformarán la comunidad, favoreciendo las optimizaciones locales de modularidad. Después de que esta asignación sea ejecutada, se define una nueva red de datos basada en las comunidades que fueron encontradas en la etapa inicial.
Estos dos pasos son repetidos una y otra vez hasta que es imposible detectar nuevas reasignaciones de comunidades que aumenten la modularidad.
Casos de uso del algoritmo de Louvain
Este algoritmo posee propiedades extremadamente interesantes que permiten construir comunidades conectadas de datos muy útiles para encontrar datos relacionados dentro de sistemas de recomendación en linea. Un caso muy especifico sería la utilización del algoritmo para encontrar temas similares o relacionados dentro de un sitio web colaborativo. También tiene su rango de aplicabilidad dentro de plataformas de contenidos o redes sociales como Twitter o Youtube sirviendo para analizar la coincidencia de términos en documentos o archivos, como parte del proceso de modelado de temas.
El método que rige al algoritmo de Louvain adicionalmente posee una potencialidad increíble para entender estructuras complejas. Es por esto que ha sido utilizado para estudiar el cerebro humano y encontrar estructuras jerárquicas de la comunidad dentro de una red de conexiones que funciona dentro de nuestro cerebro y que controla todos los aspectos funcionales del mismo.
Restricciones
Aunque estos algoritmos son muy potentes cuando se estudian amplios volúmenes de datos pueden surgir algunos problemas. Este método algorítmico posee un limite de resolución que no permite que detecten pequeñas comunidades dentro de grandes redes de datos producto de una falla general que se produce al ejecutar una optimización de modularidad.
Como habéis visto en la explicación de cómo se aplica el algoritmo, al pasar a la segunda fase de agrupación, las comunidades más grandes de datos conectados se fusionan, lo que puede ocasionar que desaparezcan del análisis comunidades conectadas de menor tamaño.
Adicionalmente a esto puede presentarse un problema de degeneración en el análisis si se presenta una red extremadamente grande ya que pueden existir grandes cantidades de soluciones de alta modularidad, convirtiéndose entonces en el proceso de encontrar el máximo global de la red en algo extremadamente complejo y difícil de valorar.
Ejemplo de aplicación
Para comprender de mejor manera el funcionamiento del algoritmo, vamos a desarrollar un ejemplo sobre un conjunto de datos determinado, analizándolo en Neo4j . Se analizará un grafo que contiene la información de un numero de personas y que poseen relaciones entre algunos de ellos. Una vez definido el conjunto de datos a estudiar procedemos a construir el grafo de la siguiente manera;
MERGE (nAlice:User {id:'Alice'})
MERGE (nBridget:User {id:'Bridget'})
MERGE (nCharles:User {id:'Charles'})
MERGE (nDoug:User {id:'Doug'})
MERGE (nMark:User {id:'Mark'})
MERGE (nMichael:User {id:'Michael'})
MERGE (nAlice)-[:FRIEND]->(nBridget)
MERGE (nAlice)-[:FRIEND]->(nCharles)
MERGE (nMark)-[:FRIEND]->(nDoug)
MERGE (nBridget)-[:FRIEND]->(nMichael)
MERGE (nCharles)-[:FRIEND]->(nMark)
MERGE (nAlice)-[:FRIEND]->(nMichael)
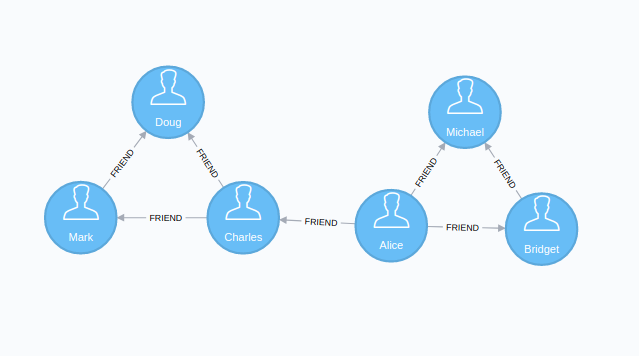
MERGE (nCharles)-[:FRIEND]->(nDoug);La representación de este grafo sería:
Una vez empieza a ejecutarse el algoritmo obtenemos una respuesta similar a la siguiente:
CALL algo.louvain.stream('User', 'FRIEND', {})
YIELD nodeId, community
RETURN algo.asNode(nodeId).id AS user, community
ORDER BY community;Al culminar el proceso de análisis de los datos se obtiene que;
CALL algo.louvain('User', 'FRIEND',
{write:true, writeProperty:'community'})
YIELD nodes, communityCount, iterations, loadMillis, computeMillis, writeMillis;Tabla de resultados del algoritmo
| Name | Community |
|---|---|
| Alice | 0 |
| Bridget | 0 |
| Michael | 0 |
| Charles | 1 |
| Doug | 1 |
| Mark | 1 |
El resultado del algoritmo nos muestra claramente que dentro del conjunto de datos que contiene el grafo analizado existen dos comunidades conectadas.
Esperamos que esta información sea de utilidad para entender de mejor manera el funcionamiento del algoritmo de Louvain.
Visita más de Grapheverywhere para conocer todo lo que necesitas sobre algoritmos y sus aplicaciones.