La centralidad armónica también conocida como centralidad varolada, es una variación desarrollada tomando como base la centralidad de proximidad. Esta es utilizada para darle respuesta a una carencia analítica del modelo original para analizar datos que contenidos en grafos no conectados, resultando de mucha utilidad para el análisis de datos provenientes de las redes sociales.

A continuación abordaremos el concepto y algunos parámetros de funcionamiento de los algoritmos de centralidad armónica.

 ¿Qué son los algoritmos de centralidad armónica?

Estos son algoritmos destinados a estudiar los datos contenidos en grafos, especialmente en grafos no conectados para estimar de forma eficiente los caminos más cortos de difusión de un conjunto de información a través de un vértice determinado en un grafo.

Este algoritmo mediante una modificación en el método de calculo de los algoritmos de centralidad de cercanía en lugar de sumar las distancias de un nodo a todos los demás nodos que conforman el grafo, suma el inverso de estas distancias y de esta manera puede estimar con eficiencia, lo que en el algoritmo de centralidad por proximidad arrojaría un valor infinito. Este algoritmo de gran utilidad e interés se encuentra dentro de la biblioteca de Neo4j y no es generalmente aceptado.

Formula de calculo

Para poder lidiar con estos valores infinitos se construye la siguiente formula que permite calcular la centralidad armónica:

Centralidad armónica bruta (nodo) = suma (1 / distancia desde el nodo a cualquier otro nodo, excluyéndose a sí mismo)

De igual forma, con la centralidad de cercanía podemos realizar el calculo de una medida de centralidad armónica normalizada si se aplica la formula  que presentamos a continuación:

Centralidad armónica normalizada (nodo) = suma (1 / distancia del nodo a cualquier otro nodo, excluyéndose a sí mismo) / (número de nodos – 1)

Casos de uso de los algoritmos de centralidad armónica

Al ser una variante de la centralidad por proximidad para casos en los que la formula original no puede detectar el rango de los datos, al caer en un calculo de dimensiones infinitos, los usos suelen ser similares pero aplicados a grafos no conectados.

Por ejemplo, este tipo de algoritmos podría ser utilizado para identificar espacios públicos dentro de una ciudad para instalar un nuevo servicio de fácil acceso a los residentes. Al detectar el grado alto de centralidad, podemos estimar donde podría beneficiarse mayor cantidad de personas. Adicionalmente si llevamos este modelo de algoritmo a redes sociales podemos estimar con mayor eficiencia los contactos o cuentas que pueden difundir la información con mayor eficiencia dentro de un segmento estimado de la red.

Ejemplo de aplicación

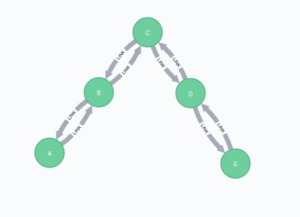
Para iniciar con el calculo de la centralidad de este tipo de algoritmo debemos construir primero un grafo similar al que te mostramos a continuación:

MERGE (a:Node{id:"A"})
MERGE (b:Node{id:"B"})
MERGE (c:Node{id:"C"})
MERGE (d:Node{id:"D"})
MERGE (e:Node{id:"E"})

MERGE (a)-[:LINK]->(b)
MERGE (b)-[:LINK]->(c)
MERGE (d)-[:LINK]->(e);

Al ejecutar el algoritmo, nos va a entregar un resultado parecido al siguiente:

CALL algo.closeness.harmonic.stream('Node', 'LINK') YIELD nodeId, centrality
RETURN nodeId,centrality
ORDER BY centrality DESC
LIMIT 20;

Para finalizar la ejecución del algoritmo obtenemos como resultado final:

CALL algo.closeness.harmonic('Node', 'LINK', {writeProperty:'centrality'})
YIELD nodes,loadMillis, computeMillis, writeMillis;

Entonces podremos expresar el resultado del calculo del algoritmo en una matriz de este tipo.

    A     B     C     D     E
 ---|-----------------------------
 A  | 0     1     2     -     -    // distance between each pair of nodes
 B  | 1     0     1     -     -    // or infinite if no path exists
 C  | 2     1     0     -     -
 D  | -     -     -     0     1
 E  | -     -     -     1     0
 ---|------------------------------
 A  | 0     1    1/2    0     0    // inverse
 B  | 1     0     1     0     0
 C  |1/2    1     0     0     0
 D  | 0     0     0     0     1
 E  | 0     0     0     1     0
 ---|------------------------------
sum |1.5    2    1.5    1     1
 ---|------------------------------
 *k |0.37  0.5  0.37  0.25  0.25

El resultado del calculo del algoritmo nos hace ver que el nodo con mayor nivel de centralidad armónica y por ende, el más funcional para transmitir información al resto del grafo es el que esta identificado como letra B.

Esperamos que esta información sobre los algoritmos de centralidad valorada o armónica te permitan comprender su funcionalidad y posibilidades de implementación.

Visita más de Grapheverywhere para conocer todo lo que necesitas sobre algoritmos de grafos.